Simple Example

This example is supposed to serve as a quick start to the ConstructTerms module of FlavorPy.

We determine the symmetry invariant terms of the flavor model introduced in “Are neutrino masses modular forms?” by F. Feruglio (https://arxiv.org/pdf/1706.08749) as so-called Example 1 in section 3.12. The chiral supermultiplets and their transformation properties of this model are

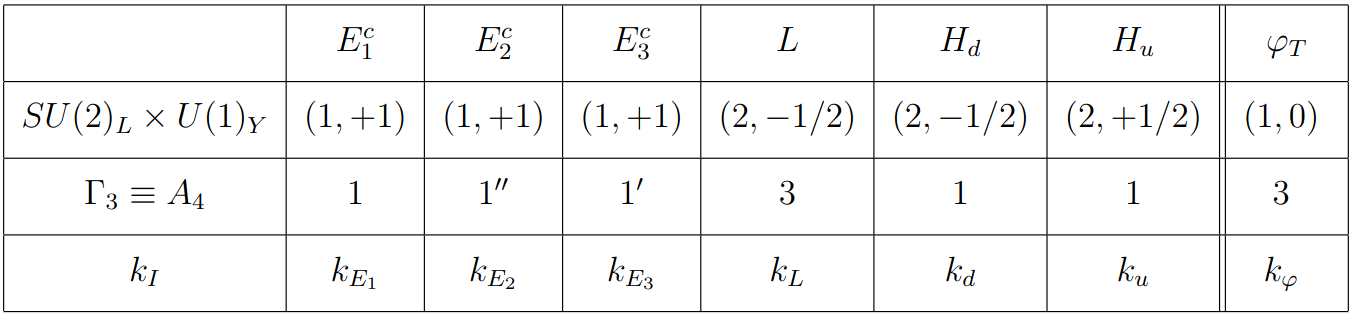
where \(k_L=1\), \(k_u=0\), \(k_\varphi=-3\), and \(k_{E_i}+k_L+k_d+k_\varphi=0\). Table taken from https://arxiv.org/pdf/1706.08749.

Import

After installing FlavorPy with pip install flavorpy, import the modelfitting module.

# Import the constructterms module of FlavorPy
import flavorpy.constructterms as ct

Define Groups

Let us start by defining the non-Abelian group \(A_4\).

# Representations of A4
A4_reps = ['1', '1p', '1pp', '3']

# Tensor products of A4_reps as a matrix, i.e. A_tensor_procuts[i,j] = A4_reps[i] x A4_reps[j]
A4_tensor_products = [[['1'], ['1p'], ['1pp'], ['3']],
                      [['1p'], ['1pp'], ['1'], ['3']],
                      [['1pp'], ['1'], ['1p'], ['3']],
                      [['3'], ['3'], ['3'], ['1', '1p', '1pp', '3', '3']]]

# Construct the group
A4 = ct.NonAbelianGroup('A4', representations=A4_reps, tensor_products=A4_tensor_products)

Next, we also need the modular weight. Since modular weights multiply in the same way as charges of a U(1) group, we can define the modular weight as a U(1) group

mod_weight = ct.U1Group('mod weight')

It often also helps to define the gauge \(U(1)_Y\) for the hypercharge

U1y = ct.U1Group('U1y')

Define Fields

Next, we can define the fields of the flavor model.

The paper does not explicitly specifies the modular weight of \(E_1^c\), \(E_2^c\), \(E_3^c\), and \(H_d\), it only says that \(k_{E_i}+k_L+k_d+k_\phi=0\). Hence we choose them accordingly.

ke = 20
kd = - ke + 1 - 3

E1 = ct.Field('E1', charges={A4:['1'], mod_weight:ke, U1y:1})
E2 = ct.Field('E2', charges={A4:['1pp'], mod_weight:ke, U1y:1})
E3 = ct.Field('E3', charges={A4:['1p'], mod_weight:ke, U1y:1})
L = ct.Field('L', charges={A4:['3'], mod_weight:-1, U1y:-1/2})
Hd = ct.Field('Hd', charges={A4:['1'], mod_weight:kd, U1y:-1/2})
Hu = ct.Field('Hu', charges={A4:['1'], mod_weight:0, U1y:+1/2})
PhiT = ct.Field('PhiT', charges={A4:['3'], mod_weight:3, U1y:0})
Y = ct.Field('Y', charges={A4:['3'], mod_weight:2, U1y:0})

all_fields = [E1, E2, E3, L, Hd, Hu, PhiT, Y]

We also need to define the superpotential as a “Field”

W = ct.Field('W', charges={A4:['1'], mod_weight:0, U1y:0})

Determine symmetry invariant terms in the superpotential

Then we can determine the symmetry invariant terms up to a specific order of the superpotential with

allowed_terms = ct.list_allowed_terms(all_fields, W, order=5)
allowed_terms

[L L Hu Hu Y, E1 L Hd PhiT, E2 L Hd PhiT, E3 L Hd PhiT]

Hence, these four terms are the only symmetry invariant terms in the superpotential up to order 5. Note that this is exactly the same result as in the paper, see eqs. (35) and (37)